Semana # 34 - 36
Tema: EL PLANO CARTESIANO

Cada punto P viene determinado por un par de números: (abscisa, ordenada), que llamamos coordenadas cartesianas del punto P. Convenimos en nombrar a la abscisa con la letra X, y a la ordenada con Y.
Los ejes se dividen en segmentos de igual longitud y a cada marca del segmento se le asigna un número entero.

En la recta horizontal (llamada "eje de abscisas" o "eje de las X"), al punto de corte con la otra recta se le asigna el 0 y hacia la derecha el 1, 2,...; y hacia la izquierda el -1, -2,... y así sucesivamente en ambas direcciones.
De forma análoga se procede con la recta vertical (llamada "eje de ordenadas" o "eje de las Y"), al punto de corte se le asigne el 0 y hacia arriba el 1,2,....; y hacia abajo el -1,-2,... etc.
De este modo cada punto del plano se localiza mediante dos números, uno correspondiente a cada eje, que se escriben encerrados entre paréntesis y separados por una coma (,) . Dicho par de números se llaman coordenadas.
Y se obtienen, por ejemplo, de la siguiente manera: el punto de coordenadas (2,3) se localiza situándonos en el punto marcado con el 2 en el eje de las "X"; una vez aquí, subimos hacia arriba verticalmente de forma paralela al eje de las "Y", hasta el lugar marcado en este eje con el 3, ese es el punto buscado. De igual forma para el punto (-3,2), nos situamos en la marca -3 del eje "X" y subimos verticalmente hasta el 2 del eje "Y".
Lógicamente el (0,0) es el punto donde se cortan los dos ejes y se llama "origen de coordenadas".
Los ejes dividen al plano en cuatro regiones que llamaremos cuadrantes.
Semana # 33
Tema: Longitud y unidades de medida
INTRODUCCIÓN:
Medir es comparar una magnitud con otra que llamamos unidad. La medida es el número de veces que la magnitud contiene a la unidad
El Sistema Métrico Decimal es un sistema de unidades en el cual los múltiplos y submúltiplos de una unidad de medida están relacionadas entre sí por múltiplos o submúltiplos de 10.
El Sistema Métrico Decimal lo utilizamos en la medida de las siguientes magnitudes:
- Longitud
- Masa
- Capacidad
- Superficie
- Volumen
Las unidades de tiempo no son del Sistema Métrico Decimal, ya que están relacionadas entre sí por múltiplos o submúltiplos de 60. El tiempo es una magnitud del Sistema Sexagesimal.
Unidades de medida de longitud
La unidad principal para medir longitudes es el metro
Está dividido en decímetros (dm), centímetros ( cm), milímetros (mm). Son sus submúltiplos
El kilómetro (km), hectómetro (hm) y el decámetro (dam), son unidades más grandes por lo tanto son sus múltiplos

¿Para qué utilizamos el metro?
El metro es empleado para medir el largo, ancho, y la altura de las cosas, es decir el metro se utiliza para conocer longitudes.

¿Cómo convertir las unidades de longitud en una más grande o más pequeña?
Cada unidad de longitud es igual a 10 unidades de orden inmediato inferior, o también cada unidad de un orden es 10 veces menor que la del orden inmediato superior.
Para pasar de una unidad a otra podemos seguir este esquema:

Semana # 31
Tema: La división
¿Qué es la división?
¿Te has dado cuenta que en más de alguna ocasión has tenido que dividir sin saber que lo estás haciendo? Por ejemplo, cuándo compartes un chocolate, o cuando en tu casa dividen la comida según la cantidad de habitantes.
La división está presente en varios ámbitos de nuestra vida y podríamos definirla como una operación aritmética de descomposición que consiste en averiguar cuántas veces un número (el divisor) está contenido en otro número (el dividendo).
Podemos decir entonces que la división forma parte de la aritmética y es inversa a la multiplicación.
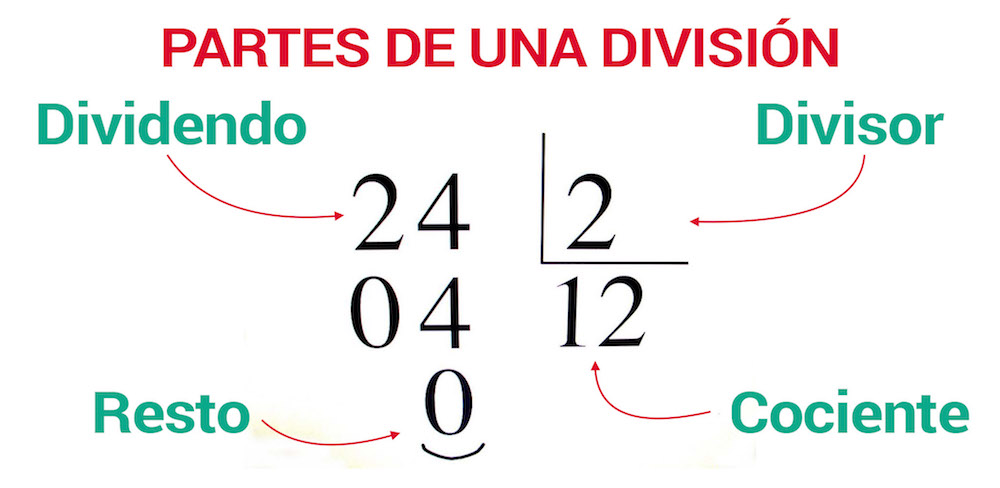
Términos de la división
En una división de números naturales, sus términos se llaman dividendo y divisor y su resultado se llama cociente. Si la división no es exacta, se obtiene un resto que es menor que el divisor y distinto de cero.
- Dividendo: es el total que vamos a dividir.
- Divisor: es la cantidad por la cual se va a dividir al total.
- Cociente: es el resultado de la operación. Éste indica la cantidad der veces que el divisor “cabe” dentro del dividendo.
- Resto: es la parte que no se ha podido distribuir. Si el resto es diferente de cero, decimos que es una división inexacta.
Semana #30
Tema: Sólidos geométricos: elementos y desarrollo plano.
Actividad: Pon en practica tus competencias, ingresa a los link sugeridos y resuelve las situaciones que te plantean los diferentes juegos.
INGRESA AL SIGUIENTE LINK Y PON A PRUEBA TUS CONOCIMIENTOS POR MEDIO DE UN JUEGO Juguemos con los sólidos geométricos
CLASIFICA SÓLIDOS INGRESANDO A ESTE LINK: Sólidos - Clasificación
INICIA EL CUARTO PERIODO
Semana #29
Tema: Sólidos geométricos: elementos y desarrollo plano.









Semana # 27 y 28
Tema: Suma y resta de números decimales

Semana # 26
Tema: Relación entre los números decimales y los números fraccionarios

Semana # 25
Tema: los números decimales


 Semana # 23
Semana # 23
Tema: Los diagramas de barras y los pictogramas



Semana # 21 y 22
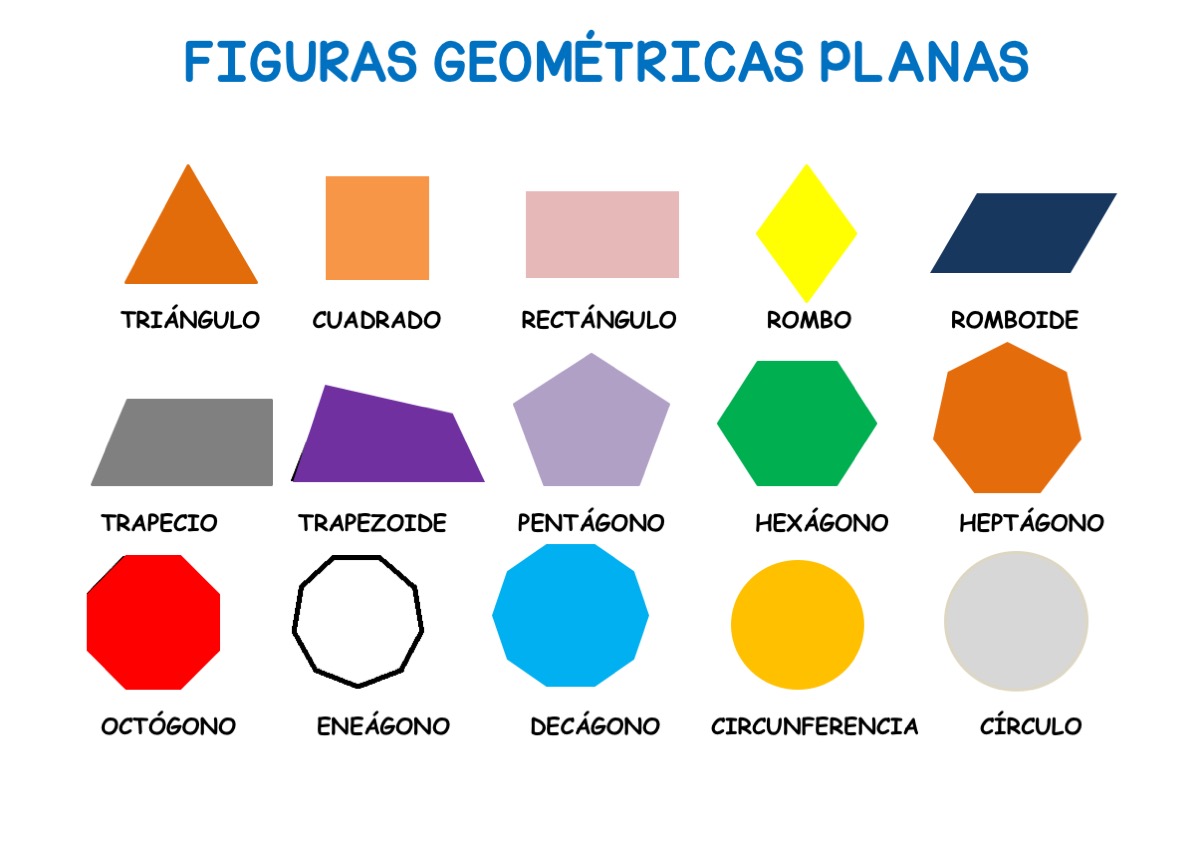
Tema: Figuras planas (polígonos convexos y no convexos)
FIGURAS PLANAS
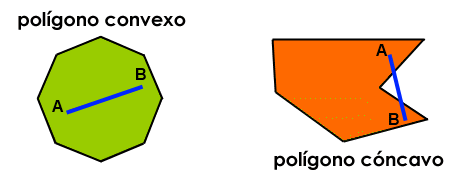
Un polígono cóncavo es una de las figuras geométricas mas interesantes que he visto y por supuesto un polígono de este tipo no es convexo.
Un polígono simple es cóncavo si y sólo si al menos uno de sus ángulos internos es mayor que 180 grados. Un ejemplo de un no-simple (auto-intersección) polígono es un polígono estrella.
Un polígono cóncavo debe tener al menos cuatro lados.
Semana # 18 y 19
Tema: Medidas de superficie planas
Semana # 16
Tema: Unidades de medida convencionales
¿Qué son las unidades de medidas?
Se denomima unidad de medida a una cantidad estandarizada de una determinada magnitud física.
Dentro de las unidades de medidas convencionales de mayor uso cotidiano, podemos destacar las siguientes:
- Unidades de longitud: cuya unidad fundamental es el metro.
- Unidades de capacidad: cuya unidad fundamental es el litro.
- Unidad de masa: cuya unidad fundamental es el kilogramo.
- Unidad de tiempo: cuya unidad fundamental es el segundo.
El Metro
El metro se define como la unidad fundamental de longitud. El metro en forma abreviada se escribe m ("m" minúscula).

¿Sabes para qué utilizamos el metro?
El metro es empleado para medir el largo, ancho, y la altura de las cosas, es decir el metro se utiliza para conocer longitudes.
Pertenecen a esta familia:
- El centímetro (cm) y milímetro (mm), que se usa para medir cosas muy chicas.
- El kilómetro (km) y el hectómetro, que se usa para medir cosas muy grandes.
Ejemplos de uso:
- Para medir tu altura y saber así cuánto has crecido (metros y centímetros).
- Para saber cuál es la distancia entre tu casa y tu colegio (kilómetros).
- Para descubrir que tan largo es un puente (metros).
El Litro:
El litro es la unidad patrón de las medidas de capacidad, su símbolo es l (una L minúscula) y se usa para calcular cualquier cantidad de líquido que hay en un recipiente.

¿Sabes para qué utilizamos el litro?
Si queremos medir el líquido que se encuentra dentro de un envase o recipiente, no podemos usar una regla o el metro, utilizamos la medida de capacidad llamada litro.
Pertenecen a esta familia
- El mililitro, que se usa para pequeñas cantidades de líquidos.
- El hectolitro, que se usa para medir grandes cantidades de líquidos.
Ejemplos de uso
- Para saber la cantidad de jugo que tiene una botella (litro).
- Para saber cuánto aceite debe tener nuestra ensalada (mililitro).
- Para conocer la cantidad de agua que necesita una piscina (hectolitro).
El Kilogramo
El kilogramo es la unidad patrón de las medidas de masa, su símbolo es kg.

¿Sabes para qué utilizamos el kilogramo?
El kilogramo es la unidad que utilizamos para medir la masa de un objeto o una cosas.
Pertenecen a esta familia:
- El miligramo, que se usa para pequeñas cantidades.
- La tonelada, que se usa para grandes cantidades.
Ejemplos de uso
- Para conocer tu peso (kilogramo).
- Para saber cuánto pesa una barra de chocolate (miligramo).
- Para saber cuánto pesa un camión (tonelada).
Semana # 15
Tema: Unidades convencionales del tiempo
Actividad: Observa atentamente el vídeo y determina las diferentes formas de medir el tiempo creadas por los seres humanos.
El instrumento que utilizamos para medir el tiempo es el reloj. La unidad que utilizaremos como referencia será el día. Con respecto al día, hay unidades de tiempo menores y mayores que el día.
Unidades más pequeñas que el día:
Un día tiene 24 horas.
Una hora tiene 60 minutos.
Un minuto tiene 60 segundos.
Unidades más grandes que el día:
7 días forman una semana.
Entre 28 y 31 días forman un mes.
12 meses forman un año.
5 años forman un lustro.
10 años forman una década.
100 años forman un siglo.
Hay muchas más unidades de medida de tiempo pero estas son las más usadas.

¿Cómo podemos pasar de una unidad de tiempo a otra? Para cambiar de unas unidades a otras hay que utilizar el sistema sexagesimal porque 60 segundos es 1 minuto y 60 minutos es 1 hora.
En la siguiente imagen se puede ver que para pasar de días a minutos horas a minutos hay que multiplicar por 60 y para pasar de minutos a segundos también hay que multiplicar por 60. Por otro lado, para pasar de segundos a minutos hay que dividir entre 60 y para pasar de minutos a horas también hay que dividir entre 60.
Semana # 14
Tema: Solucionemos problemas
Actividad: Observa detenidamente el vídeo, encuentra claves o estrategias para que los uses al realizar problemas matemáticos.
Semana # 13
Tema: La multiplicación
Multiplicar es lo mismo que sumar varias veces el mismo número.
Por ejemplo:
2 x 3 es lo mismo que sumar el número 2 tres veces (2 + 2+ 2)
6 x 5 es lo mismo que sumar el número 6 cinco veces (6 + 6 + 6 + 6 + 6)
Cuando vamos a hacer una multiplicación, por ejemplo 5 x 3, la escribimos de la siguiente manera:
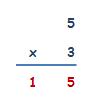
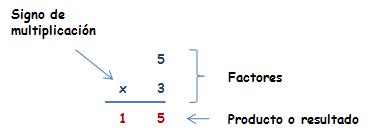
Los términos de la multiplicación son: Factores y Producto (o resultado).
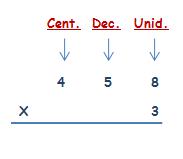
Vamos a hacer una multiplicación: 458 x 3.
Tenemos que multiplicar el 3 por cada cifra de 458, empezando por las unidades, después por las decenas y después por las centenas
Multiplicamos el 3 por las unidades:
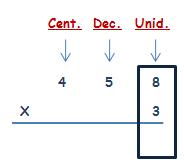
3 x 8 es igual a 24:
24 tiene dos cifras, tan sólo escribimos en el resultado la primera cifra de la derecha (4). La otra cifra (2) se la vamos a sumar al resultado de multiplicar 3 por las decenas:

3 x 5 es igual a 15; le sumamos 2 y nos da 17:
Al igual que vimos antes, 17 tiene 2 cifras, en el resultado tan sólo escribimos la primera cifra de la derecha (7); la otra cifra (1) se la vamos a sumar al resultado de multiplicar 3 por las centenas:

3 x 4 es igual a 12; le sumamos 1 y nos da 13. Como ya no quedan más cifras por multiplicar ahora si escribimos en el resultado el número entero (13):

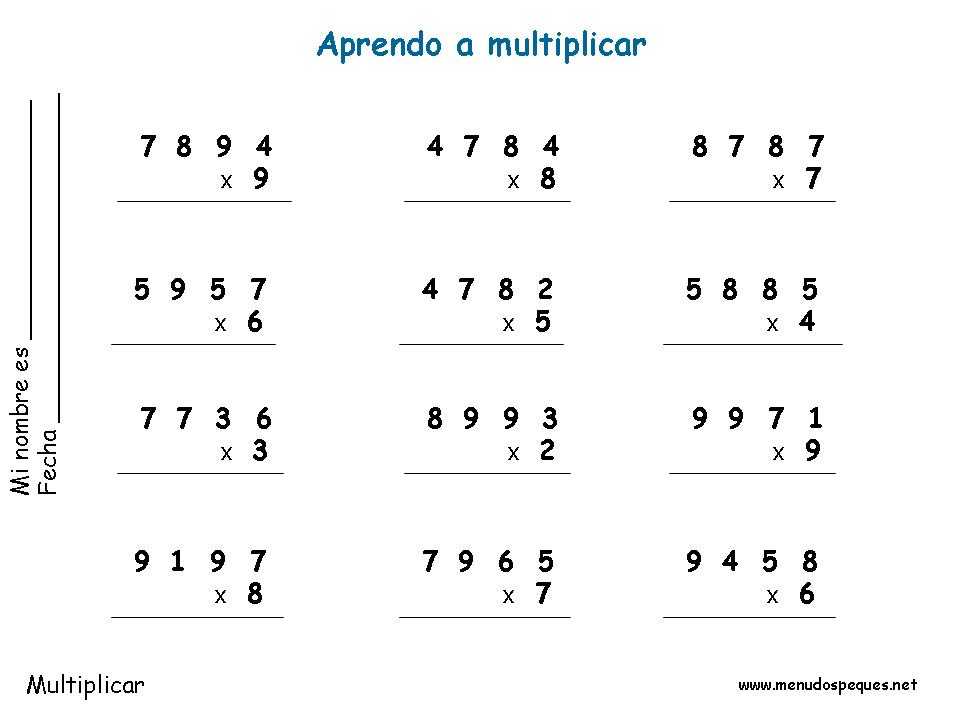
Resuelve:
Semana # 11 y 12
Tema: Fracciones equivalentes









INICIA EL SEGUNDO PERIODO
Semana # 8 y 9
Tema: Tipos de fracciones
Semana # 7
Tema: Sistema de numeración decimal y operaciones entre dichos números.
Actividad: ingresa al siguiente enlace e interactua con los números a través de juegos.
JUEGOS MATEMÁTICOS
Semana # 6
Tema: La adición y la sustracción
Actividad: realiza en clases las actividades sugeridas por la docente.


Semana # 5
Tema: La sustracción y sus términos
Actividad: observa el siguiente vídeo y escribe los aspectos más relevantes en tu cuaderno.
Semana # 4
Tema: Propiedades de la Adición
Semana # 3
Tema: ¿Cómo se miden un ángulos y cómo usar el transportador?
Actividad: Observa el vídeo y pon en practica lo aprendido.
Tema: El valor posicional
El valor posicional es el valor que toma un dígito de acuerdo con la posición que ocupa dentro del número (unidades, decenas, centenas…). Es por ello que el cambio de posición de un dígito dentro de un número altera el valor total del mismo.

Semana # 2
Tema: EL PLANO CARTESIANO
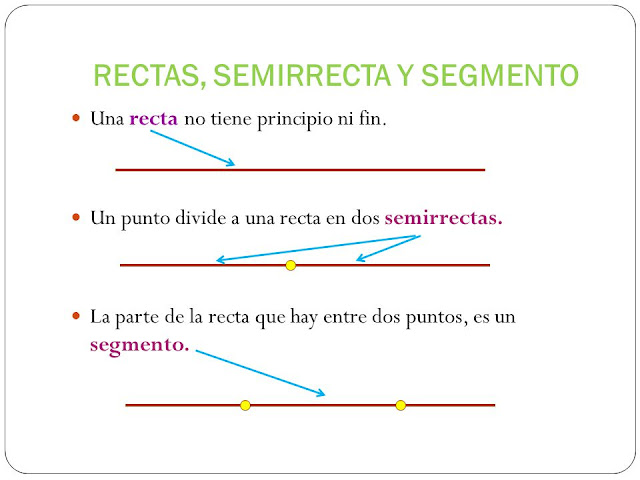
Para localizar un punto en el plano utilizamos dos rectas perpendiculares entre sí, llamadas ejes, uno horizontal que llamamos de “abscisas” y otro vertical de “ordenadas”, que se cortan en un punto “el origen de coordenadas”, llamado.

Cada punto P viene determinado por un par de números: (abscisa, ordenada), que llamamos coordenadas cartesianas del punto P. Convenimos en nombrar a la abscisa con la letra X, y a la ordenada con Y.
Los ejes se dividen en segmentos de igual longitud y a cada marca del segmento se le asigna un número entero.

En la recta horizontal (llamada "eje de abscisas" o "eje de las X"), al punto de corte con la otra recta se le asigna el 0 y hacia la derecha el 1, 2,...; y hacia la izquierda el -1, -2,... y así sucesivamente en ambas direcciones.
De forma análoga se procede con la recta vertical (llamada "eje de ordenadas" o "eje de las Y"), al punto de corte se le asigne el 0 y hacia arriba el 1,2,....; y hacia abajo el -1,-2,... etc.
De este modo cada punto del plano se localiza mediante dos números, uno correspondiente a cada eje, que se escriben encerrados entre paréntesis y separados por una coma (,) . Dicho par de números se llaman coordenadas.
Y se obtienen, por ejemplo, de la siguiente manera: el punto de coordenadas (2,3) se localiza situándonos en el punto marcado con el 2 en el eje de las "X"; una vez aquí, subimos hacia arriba verticalmente de forma paralela al eje de las "Y", hasta el lugar marcado en este eje con el 3, ese es el punto buscado. De igual forma para el punto (-3,2), nos situamos en la marca -3 del eje "X" y subimos verticalmente hasta el 2 del eje "Y".
Lógicamente el (0,0) es el punto donde se cortan los dos ejes y se llama "origen de coordenadas".
Los ejes dividen al plano en cuatro regiones que llamaremos cuadrantes.
Semana # 33
Tema: Longitud y unidades de medida
LA LONGITUD Y SUS UNIDADES DE MEDIDA
INTRODUCCIÓN:
Medir es comparar una magnitud con otra que llamamos unidad. La medida es el número de veces que la magnitud contiene a la unidad
El Sistema Métrico Decimal es un sistema de unidades en el cual los múltiplos y submúltiplos de una unidad de medida están relacionadas entre sí por múltiplos o submúltiplos de 10.
El Sistema Métrico Decimal lo utilizamos en la medida de las siguientes magnitudes:
- Longitud
- Masa
- Capacidad
- Superficie
- Volumen
Las unidades de tiempo no son del Sistema Métrico Decimal, ya que están relacionadas entre sí por múltiplos o submúltiplos de 60. El tiempo es una magnitud del Sistema Sexagesimal.
Unidades de medida de longitud
La unidad principal para medir longitudes es el metro
Está dividido en decímetros (dm), centímetros ( cm), milímetros (mm). Son sus submúltiplos
El kilómetro (km), hectómetro (hm) y el decámetro (dam), son unidades más grandes por lo tanto son sus múltiplos

¿Para qué utilizamos el metro?
El metro es empleado para medir el largo, ancho, y la altura de las cosas, es decir el metro se utiliza para conocer longitudes.
¿Cómo convertir las unidades de longitud en una más grande o más pequeña?
Cada unidad de longitud es igual a 10 unidades de orden inmediato inferior, o también cada unidad de un orden es 10 veces menor que la del orden inmediato superior.
Para pasar de una unidad a otra podemos seguir este esquema:

Semana # 31
Tema: La división
¿Te has dado cuenta que en más de alguna ocasión has tenido que dividir sin saber que lo estás haciendo? Por ejemplo, cuándo compartes un chocolate, o cuando en tu casa dividen la comida según la cantidad de habitantes.
La división está presente en varios ámbitos de nuestra vida y podríamos definirla como una operación aritmética de descomposición que consiste en averiguar cuántas veces un número (el divisor) está contenido en otro número (el dividendo).
Podemos decir entonces que la división forma parte de la aritmética y es inversa a la multiplicación.
Términos de la división
En una división de números naturales, sus términos se llaman dividendo y divisor y su resultado se llama cociente. Si la división no es exacta, se obtiene un resto que es menor que el divisor y distinto de cero.
- Dividendo: es el total que vamos a dividir.
- Divisor: es la cantidad por la cual se va a dividir al total.
- Cociente: es el resultado de la operación. Éste indica la cantidad der veces que el divisor “cabe” dentro del dividendo.
- Resto: es la parte que no se ha podido distribuir. Si el resto es diferente de cero, decimos que es una división inexacta.

Semana #30
Tema: Sólidos geométricos: elementos y desarrollo plano.
Actividad: Pon en practica tus competencias, ingresa a los link sugeridos y resuelve las situaciones que te plantean los diferentes juegos.
INGRESA AL SIGUIENTE LINK Y PON A PRUEBA TUS CONOCIMIENTOS POR MEDIO DE UN JUEGO Juguemos con los sólidos geométricos
CLASIFICA SÓLIDOS INGRESANDO A ESTE LINK: Sólidos - Clasificación
Ahora, ubica cada una de las partes de los siguientes sólidos (ingresa al link) PARTES DE LOS SÓLIDOS
INICIA EL CUARTO PERIODO
Semana #29
Tema: Sólidos geométricos: elementos y desarrollo plano.
¿Qué son los cuerpos geométricos?
Un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia, tienen un volumen.

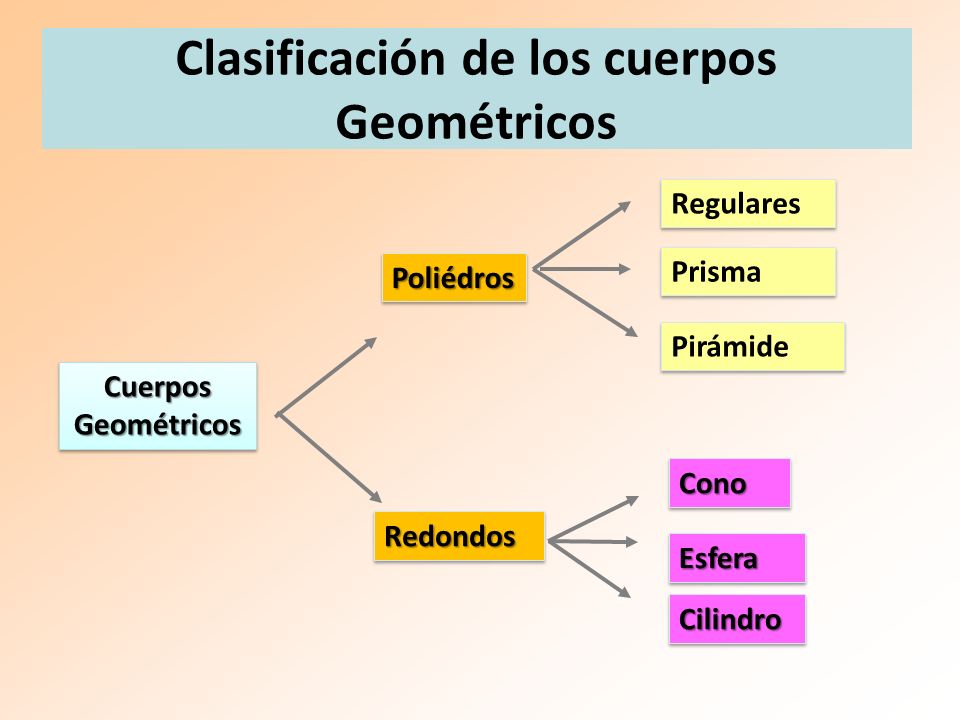
Los cuerpos geométricos pueden ser: Poliedros y Cuerpos Redondos.
Poliedros:
Son sólidos geométricos de muchas caras, que contienen los siguientes elementos: caras, aristas, vértices.
Caras:
Son las superficies planas que forman el poliedro, las cuales se interceptan entre sí.

Aristas:
Son los segmentos formados por la intersección de dos (2) caras.


Vértices:
Son los puntos donde se interceptan 3 o más aristas.



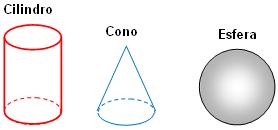
Cuerpos redondos:
Son cuerpos geométricos compuestos total o parcialmente por figuras geométricas curvas; como por ejemplo el cilindro, la esfera o el cono.
Reconozcamos los cuerpos redondos en nuestro entorno:
En nuestro entorno podemos encontrar muchas formas.¿Reconoces alguna?
Recuerda que los cuerpos redondos tienen superficies curvas.
Algunos ejemplos que podemos encontrar en nuestro entorno son:



Tema: Suma y resta de números decimales

Semana # 26
Tema: Relación entre los números decimales y los números fraccionarios
Semana # 25
Tema: los números decimales
Números Decimales
Los números decimales son valores que denotan números racionales e irracionales, es decir que los números decimales son la expresión de números no enteros, que a diferencia de los números fraccionarios, no se escriben como el cociente de dos números enteros sino como una aproximación de tal valor.
¿Qué son números decimales?
Un número decimal, por definición, es la expresión de un número no entero, que tiene una parte decimal. Es decir, que cada número decimal tiene una parte entera y una parte decimal que va separada por una coma, y son una manera particular de escribir las fracciones como resultado de un cociente inexacto.
La décima
La décima es un valor más pequeño que la unidad
1 unidad = 10 décimas.
Es decir, si dividimos una unidad en 10 partes iguales, cada una de ellas es una décima.
Las décimas van a la derecha de la coma.
La centésima
Es un valor más pequeño que la unidad y también que la décima.
1 unidad = 100 centésimas
1 décima = 10 centésimas.
Es decir, si dividimos una unidad en 100 partes iguales, cada una de ellas es una centésima.
Y si dividimos una décima en 10 partes iguales, cada una de ellas es una centésima.
La milésima
Es un valor más pequeño que la unidad, que la décima y también que la centésima:
1 unidad = 1.000 milésimas
1 décima = 100 milésimas
1 centésima = 10 milésimas
Es decir, si dividimos una unidad en 1.000 partes iguales, cada una de ellas es una centésima.
VALOR PROPOSICIONAL EN LOS NÚMEROS
DECIMALES
Tema: Los diagramas de barras y los pictogramas
Un diagrama de barras, también conocido como gráfico de barras o diagrama de columnas, es una forma de representar gráficamente un conjunto de datos o valores, y está conformado por barras rectangulares de longitudes proporcionales a los valores representados.
Una tabla gráfica es una visualización de resumen diseñada para ofrecer mucha información de un solo vistazo. Se puede configurar para que muestre columnas con elementos dinámicos como minigráficos, valores calculados o iconos condicionales. Se muestra un valor por cada fila como se especifica en el eje Filas.
¿Qué es un pictograma?
Un pictograma es un tipo de gráfico cuya información se grafica a través de dibujos.
Por ejemplo:
María encuestó a sus compañeros respecto a sus lugares preferidos para pasear. Con los datos, construyó el siguiente pictograma.

Semana # 21 y 22
Tema: Figuras planas (polígonos convexos y no convexos)
FIGURAS PLANAS

POLÍGONOS CONVEXOS Y NO CONVEXOS
Un polígono simple es cóncavo si y sólo si al menos uno de sus ángulos internos es mayor que 180 grados. Un ejemplo de un no-simple (auto-intersección) polígono es un polígono estrella.
Un polígono cóncavo debe tener al menos cuatro lados.

Semana # 18 y 19
Tema: Medidas de superficie planas
Semana # 16
Tema: Unidades de medida convencionales
¿Qué son las unidades de medidas?
Se denomima unidad de medida a una cantidad estandarizada de una determinada magnitud física.
Dentro de las unidades de medidas convencionales de mayor uso cotidiano, podemos destacar las siguientes:
- Unidades de longitud: cuya unidad fundamental es el metro.
- Unidades de capacidad: cuya unidad fundamental es el litro.
- Unidad de masa: cuya unidad fundamental es el kilogramo.
- Unidad de tiempo: cuya unidad fundamental es el segundo.
El Metro
El metro se define como la unidad fundamental de longitud. El metro en forma abreviada se escribe m ("m" minúscula).

¿Sabes para qué utilizamos el metro?
El metro es empleado para medir el largo, ancho, y la altura de las cosas, es decir el metro se utiliza para conocer longitudes.
Pertenecen a esta familia:
- El centímetro (cm) y milímetro (mm), que se usa para medir cosas muy chicas.
- El kilómetro (km) y el hectómetro, que se usa para medir cosas muy grandes.
Ejemplos de uso:
- Para medir tu altura y saber así cuánto has crecido (metros y centímetros).
- Para saber cuál es la distancia entre tu casa y tu colegio (kilómetros).
- Para descubrir que tan largo es un puente (metros).
El Litro:
El litro es la unidad patrón de las medidas de capacidad, su símbolo es l (una L minúscula) y se usa para calcular cualquier cantidad de líquido que hay en un recipiente.

¿Sabes para qué utilizamos el litro?
Si queremos medir el líquido que se encuentra dentro de un envase o recipiente, no podemos usar una regla o el metro, utilizamos la medida de capacidad llamada litro.
Pertenecen a esta familia
- El mililitro, que se usa para pequeñas cantidades de líquidos.
- El hectolitro, que se usa para medir grandes cantidades de líquidos.
Ejemplos de uso
- Para saber la cantidad de jugo que tiene una botella (litro).
- Para saber cuánto aceite debe tener nuestra ensalada (mililitro).
- Para conocer la cantidad de agua que necesita una piscina (hectolitro).
El Kilogramo
El kilogramo es la unidad patrón de las medidas de masa, su símbolo es kg.

¿Sabes para qué utilizamos el kilogramo?
El kilogramo es la unidad que utilizamos para medir la masa de un objeto o una cosas.
Pertenecen a esta familia:
- El miligramo, que se usa para pequeñas cantidades.
- La tonelada, que se usa para grandes cantidades.
Ejemplos de uso
- Para conocer tu peso (kilogramo).
- Para saber cuánto pesa una barra de chocolate (miligramo).
- Para saber cuánto pesa un camión (tonelada).
Semana # 15
Tema: Unidades convencionales del tiempo
Actividad: Observa atentamente el vídeo y determina las diferentes formas de medir el tiempo creadas por los seres humanos.
¿Cómo podemos medir el tiempo? ¿Qué unidades se utilizan?
El instrumento que utilizamos para medir el tiempo es el reloj. La unidad que utilizaremos como referencia será el día. Con respecto al día, hay unidades de tiempo menores y mayores que el día.
Unidades más pequeñas que el día:
Un día tiene 24 horas.
Una hora tiene 60 minutos.
Un minuto tiene 60 segundos.
Unidades más grandes que el día:
7 días forman una semana.
Entre 28 y 31 días forman un mes.
12 meses forman un año.
5 años forman un lustro.
10 años forman una década.
100 años forman un siglo.
Hay muchas más unidades de medida de tiempo pero estas son las más usadas.

¿Cómo podemos pasar de una unidad de tiempo a otra? Para cambiar de unas unidades a otras hay que utilizar el sistema sexagesimal porque 60 segundos es 1 minuto y 60 minutos es 1 hora.
En la siguiente imagen se puede ver que para pasar de días a minutos horas a minutos hay que multiplicar por 60 y para pasar de minutos a segundos también hay que multiplicar por 60. Por otro lado, para pasar de segundos a minutos hay que dividir entre 60 y para pasar de minutos a horas también hay que dividir entre 60.
Semana # 14
Tema: Solucionemos problemas
Actividad: Observa detenidamente el vídeo, encuentra claves o estrategias para que los uses al realizar problemas matemáticos.
Pasos para solucionar problemas matemáticos
1. Para resolver un problema matemático lo primero que debemos identificar es qué es lo que nos están pidiendo, saber dónde queremos llegar o que debemos conseguir, es decir, identificar la incógnita, si no comprendemos este punto es muy difícil llegar a una solución para el problema. Una técnica es resumir el problema con nuestras propias palabras.
2. Otro punto muy importante es saber aplicar las operaciones matemáticas como sumas, restas multiplicaciones, divisiones y otras operaciones.
- La suma se relaciona con añadir, agregar, juntar o reunir, elementos de una misma clase.
- Restar es separar o quitar una cantidad de otra.
- Multiplicar es equivalente a sumar un número tantas veces como dice otro número, por ejemplo: Nicolás lleva 2 galletas diarias de colación al colegio ¿cuántas galletas consume a la semana? Tenemos el primer dato que son las 2 galletas y el segundo dato son los días de colegio en una semana, que son 5. Entonces la operación es 2 x 5.
- Dividir es repartir un número en varias partes iguales.
Teniendo claro a que equivale cada operación es más fácil saber cuál aplicar en cada caso.
3. Luego de entender el problema debemos identificar los datos que se nos entregan y plantearlas de acuerdo a la operación que más nos sirva.
4. Por último debemos repasar los pasos que dimos comparándolo con el problema dado para ver y comprobar si nos hemos equivocado en algo. Luego de esto podremos decir que tenemos la solución al problema.
Semana # 13
Tema: La multiplicación
¿Qué es multiplicar?
Multiplicar es lo mismo que sumar varias veces el mismo número.
Por ejemplo:
2 x 3 es lo mismo que sumar el número 2 tres veces (2 + 2+ 2)
6 x 5 es lo mismo que sumar el número 6 cinco veces (6 + 6 + 6 + 6 + 6)
Cuando vamos a hacer una multiplicación, por ejemplo 5 x 3, la escribimos de la siguiente manera:
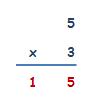
Los términos de la multiplicación son: Factores y Producto (o resultado).

Vamos a hacer una multiplicación: 458 x 3.
Tenemos que multiplicar el 3 por cada cifra de 458, empezando por las unidades, después por las decenas y después por las centenas

Multiplicamos el 3 por las unidades:

3 x 8 es igual a 24:
24 tiene dos cifras, tan sólo escribimos en el resultado la primera cifra de la derecha (4). La otra cifra (2) se la vamos a sumar al resultado de multiplicar 3 por las decenas:

3 x 5 es igual a 15; le sumamos 2 y nos da 17:
Al igual que vimos antes, 17 tiene 2 cifras, en el resultado tan sólo escribimos la primera cifra de la derecha (7); la otra cifra (1) se la vamos a sumar al resultado de multiplicar 3 por las centenas:

3 x 4 es igual a 12; le sumamos 1 y nos da 13. Como ya no quedan más cifras por multiplicar ahora si escribimos en el resultado el número entero (13):

Resuelve:

Semana # 11 y 12
Tema: Fracciones equivalentes
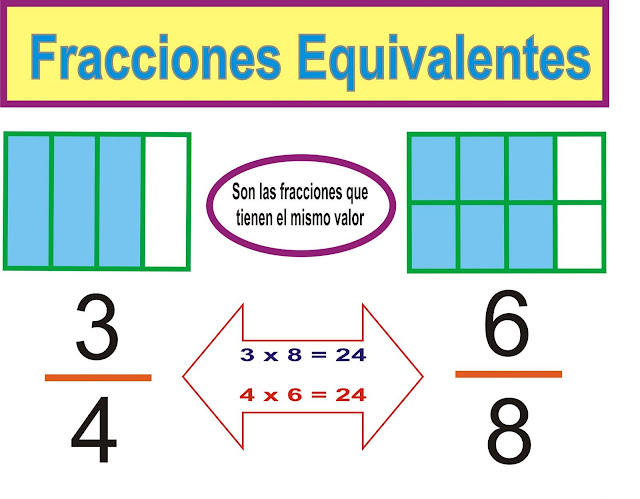
¿Qué son las fracciones equivalentes?
Las fracciones equivalentes son aquellas fracciones que representan una misma cantidad. Por ejemplo, ¿cuál de las siguientes fracciones crees que será mayor?

¿Lo has averiguado? Vamos a verlo con un ejemplo, partiendo esta pizza en tantos trozos como indique la fracción.

Para representar 1/2, partiremos la pizza en 2 trozos y nos quedaremos con 1 trozo:

Para representar 3/6, partiremos la pizza en 6 trozos y nos quedaremos con 3 trozos:

Para representar 4/8, partiremos la pizza en 8 trozos y nos quedaremos con 4 trozos:

¿Hay algún trozo de pizza que sea más grande? ¡No! Fíjate, las tres fracciones representan la misma cantidad de pizza, justo la mitad, por eso son fracciones equivalentes:

¿Cómo podemos hallar una fracción que sea equivalente a otra?
Si queremos hallar una fracción equivalente a otra, podemos:
Multiplicar denominador y numerador por el mismo número. Hallamos una fracción equivalente con numerador y denominador más grandes. Por eso este proceso se llama amplificación.

Dividir denominador y numerador por el mismo número (ambos deben ser divisibles por este número). Así, estamos hallando una fracción equivalente con numerador y denominador más pequeños. Por eso, este proceso se llama simplificación.


Actividad en el cuaderno: resuelve

Ingresa al siguiente enlace para que practiques lo aprendido:
INICIA EL SEGUNDO PERIODO
Semana # 8 y 9
Tema: Tipos de fracciones
Semana # 7
Tema: Sistema de numeración decimal y operaciones entre dichos números.
Actividad: ingresa al siguiente enlace e interactua con los números a través de juegos.
JUEGOS MATEMÁTICOS
Semana # 6
Tema: La adición y la sustracción
Actividad: realiza en clases las actividades sugeridas por la docente.


Semana # 5
Tema: La sustracción y sus términos
Actividad: observa el siguiente vídeo y escribe los aspectos más relevantes en tu cuaderno.
Semana # 4
Tema: Propiedades de la Adición
Complementa con la siguiente información:
Semana # 3
Tema: ¿Cómo se miden un ángulos y cómo usar el transportador?
Actividad: Observa el vídeo y pon en practica lo aprendido.
Tema: El valor posicional
EL VALOR POSICIONAL

Semana # 2
Tema: Elementos geométricos
Actividad: Observa detenidamente el vídeo, escribe en tu cuaderno los aspectos importantes de los elementos geométricos tratados y resuelve el taller diagnostico.








No hay comentarios:
Publicar un comentario